| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
- 주일설교
- Statistics
- 인공지능
- R
- openCV
- WebGL
- 김양재 목사
- 김양재 목사님
- Machine Learning
- No SQL
- node.js
- 데이터 과학
- Big Data
- 확률
- 몽고디비
- Deep learning
- 우리들교회
- Artificial Intelligence
- 빅데이터
- c++
- 빅 데이타
- nodeJS
- probability
- 김양재
- MongoDB
- 통계
- 빅데이타
- data science
- 빅 데이터
- 딥러닝
- Today
- Total
목록linear regression (6)
Scientific Computing & Data Science
 [Artificial Intelligence / TensorFlow] R-TensorFlow 예제 - Multi-variable Linear Regression
[Artificial Intelligence / TensorFlow] R-TensorFlow 예제 - Multi-variable Linear Regression
by Geol Choi | Jul. 8, 2017 이번 포스팅에서는 다중변수 선형 회귀(Multi-variable Linear Regression 또는 Multiple Linear Regression) 모델에 대한 간단한 이론과 이를 TensorFlow를 이용하여 최적화 문제로 풀고 결과를 비교해 보도록 하겠다.1. Theory by Example 1.1. Dataset - IQ와 신체적 특성과의 관계지능지수에 관하여 많은 사람들이 궁금해하는 것이 있다: "과연 뇌의 크기와 지능지수와의 상관성이 있을까? 있다면, 뇌의 크기로 지능지수를 유추할 수 있을까?" 이 질문에 답을 하기 위하여 몇몇 연구자들(Willerman, et al, 1991)은 38명의 대학생들을 상대로 뇌의 신체적 특성과 IQ를 조사하였..
 [Artificial Intelligence / TensorFlow] R-TensorFlow 예제 - Linear Regression
[Artificial Intelligence / TensorFlow] R-TensorFlow 예제 - Linear Regression
by Geol Choi | April 11, 2017 지난 포스팅에 이어 R-TensorFlow 세번째 예제로 Linear Regression을 구현하는 방법에 대하여 알아보기로 한다. TensorFlow 라이브러리 로딩하기지난 포스팅의 예제들과 마찬가지로 가장 먼저 할 일은, TensorFlow 라이브러리를 로딩하는 것이다. 이 외에도 Linear Regression을 시각화 하기 위해 plotly 라이브러리도 로딩하도록 한다: R CODE:# import library if (! ("plotly" %in% rownames(installed.packages()))) { install.packages("plotly") } library(plotly) if (! ("tensorflow" %in% rowna..
 [Data Science / Posts] 데이터 과학자들이 사용하는 40가지 기술
[Data Science / Posts] 데이터 과학자들이 사용하는 40가지 기술
이 글에 소개되는 기술들은 대부분의 데이터 과학자 및 관련 업계 종사자들이 매일의 업무에 사용하는 기술로써 벤더가 제공하거나 직접 설계해서 쓰는 툴들이다. 아래 40개 중 어느 링크를 클릭하면 논의가 되고 있는 관련 글을 자세하게 읽을 수 있다. 이들 대부분의 글들은 구글 검색으로는 찾기 어렵기 때문에 데이터 과학, 머신러닝, 통계 과학에 대한 숨은 문헌에 접근하는 것이 된다. 이들 중 대다수는 논의가 되고 있는 기술에 대한 근본적인 이해를 돕고자 하는 것이며, 심도있는 참고문헌 및 소스코드를 제공한다.별표(*)가 되어있는 기술들은 소위 딥 데이터 과학(Deep Data Science)에 속하며, 이는 머신러닝, 컴퓨터 과학, 오퍼레이션 연구, 수학, 통계학 등의 분야와 조금이라도 겹치는 데이터 과학의 ..
 [Artificial Intelligence] Multiple Linear Regression with R
[Artificial Intelligence] Multiple Linear Regression with R
이번 글에서는 Multiple Linear Regression(다중 선형 회귀분석)에 대한 기초 통계 이론에 대한 소개와 이에 대한 R 프로그래밍에 대해 알아보기로 한다.Theoretical Background일반적으로 얻어지는 데이터들은 여러 개의 독립변수들에 의해 얻어진다. Multiple Linear Regression은 이러한 여러 개의 독립변수(설명변수)들과 종속변수(반응변수)들 간의 관계(모델)를 도출하고, 얻어진 모델을 이용하여 특정 독립 변수에 대한 추정값을 얻는 기법이다. 다음은 n개의 독립변수들을 갖는 Multiple Linear Regression 모델이다: \( \displaystyle{ y = \beta_0 x_0 + \beta_1 x_1 + \cdots + \beta_n x_n ..
by Geol Choi | December 14, 2014 이번 글에서는 기울기 \(\beta_{1}\)에 대한 추정에 대하여 알아보도록 하자. 우선 이론적 배경을 살펴보도록 하고 R 코드를 이용하여 예제를 통해 이해하도록 한다.Theoretical Background기울기 \(\beta_{1}\)은 실험자에게 특별한 관심 대상인데, 실험 값 x와 이에 대한 결과 값 y의 상관성 지표를 나타내기 때문이다. 기울기 값에 대한 신뢰 구간(confidence interval)을 계산하는 것과 기울기 값이 특정 값을 값는 것에 대한 가설을 테스트하는 것은 매우 유용하다. \(\beta_{1}\)을 실험 데이터에 대한 알려지지 않은 참값(True Value)라고 하고 \(\hat{\beta}_1\)을 데이터 세트..
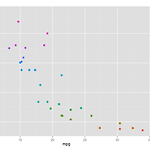 [Data Mining with R] R / Simple Linear Regression - Part 1.
[Data Mining with R] R / Simple Linear Regression - Part 1.
by Geol Choi | November 23, 2014 이번 글에서는 Linear Regression에 대한 기초 통계 이론에 대한 소개와 이에 대한 R 프로그래밍에 대해 알아보기로 한다. Linear Regression은 간단하게 말해, 관찰된 데이터들의 변수들 간 관계를 1차원적인 Graph로 표현(이를 fitting이라고 함)하는 것이다. Linear Regression은 통계학의 역사관점에서 볼 때, 특정 변수가 다른 변수와 어떤 상관관계인지를 알아보기 위한 수단으로 발전해 왔다. 데이터를 관찰하여 이에 대한 모델을 세우고 이 모델을 통해 데이터에 대한 예측을 하고자 하는 것이 목표이며, 더 나아가 이에 대한 신뢰도를 어떻게 평가할 수 있는가가 이 이론에 대한 거의 전부라고 할 수 있다. 물론..
